最小二乗法再入門 - インゲージ開発者ブログ

こんにちは。ksr_cyclです。

最近こんな素敵な本に出会いまして、読み始めているのですが、数学の基礎部分がかなり記憶から薄れていた為、その中でも最小二乗法を再入門する形で勉強しました。

最小二乗法

最小二乗法とは、データの組 $x$ と $y$ に直線的な関係をあると推察出来る時、説明変数を $x$ とし、目的変数を $y$ とした場合、説明変数から尤もらしい直線である関数 $y=f(x)$ を求める方法です。尤もらしい直線は以下の式で求めることが出来ます。

$y=Ax+B$

傾き $A$ と切片 $B$ は、それぞれ以下の式になります。

$\displaystyle{ A=\frac{Cov(x, y)}{\sigma^2_x}=\frac{\frac1n\sum_{i=1}^n(x_i-\bar{x})(y_i-\bar{y})}{\frac1n\sum_{i=1}^n(x_i-\bar{x})^2} }$

$\displaystyle{ B=\bar{y} - A\bar{x} }$

数式を解説すると、

$Cov$ : 共分散。 $x$ の偏差と $y$ の偏差を掛けて、その平均を取る。

$\displaystyle{ Cov=\frac1n\sum_{i=1}^n(x_i-\bar{x})(y_i-\bar{y}) }$

$\sigma^ 2$ : 分散。 $x$ の偏差を2乗し、その平均をとる。

$\displaystyle{ \sigma^ 2=\frac1n\sum_{i=1}^n(x_i-\bar{x})^2 }$

$\bar{x},\bar{y}$ : それぞれの平均値

$\displaystyle{ \bar{x}=\frac1n\sum_{i=1}^n x_i }$

最小二乗法は別名で回帰（線形回帰）と呼ばれ、今回の例では説明変数( $x$ )が1つとなるため、単回帰分析になります。

実装

Pythonでスクラッチ実装をすると、以下のようになります。

import numpy as np
import matplotlib.pyplot as plt


# ランダムな整数20個の配列を作る
np.random.seed(42)
X = np.random.randint(1, 20, 20)
y = np.random.randint(1, 20, 20)

# 共分散
def covariance(X, y):
    X_deviation = X - X.mean()
    y_deviation = y - y.mean()
    cov = (X_deviation * y_deviation).mean()
    return cov

# 分散
def variance(X):
    var = ((X - X.mean()) ** 2).mean()
    return var

# 上の共分散、分散を使って傾きと切片を求める関数
def least_squares_method(X, y):
    A = covariance(X, y) / variance(X)
    B = y.mean() - A * X.mean()
    return A, B

# 求められた傾きと切片から最小二乗法を適用する関数
def f(X, y):
    A, B = least_squares_method(X, y)
    return A*X + B

上の関数を使い、出力をグラフにプロットしてみます。

fig = plt.figure(figsize=(10,8))
plt.style.use('seaborn')
plt.scatter(X, y, c='r', label='(xi,yi)')
plt.plot(X, f(X, y), 'b', label='y=f(x)')
plt.xlabel('X')
plt.ylabel('y')
plt.legend(loc='upper left', bbox_to_anchor=(1,1), fontsize=16)
plt.show()

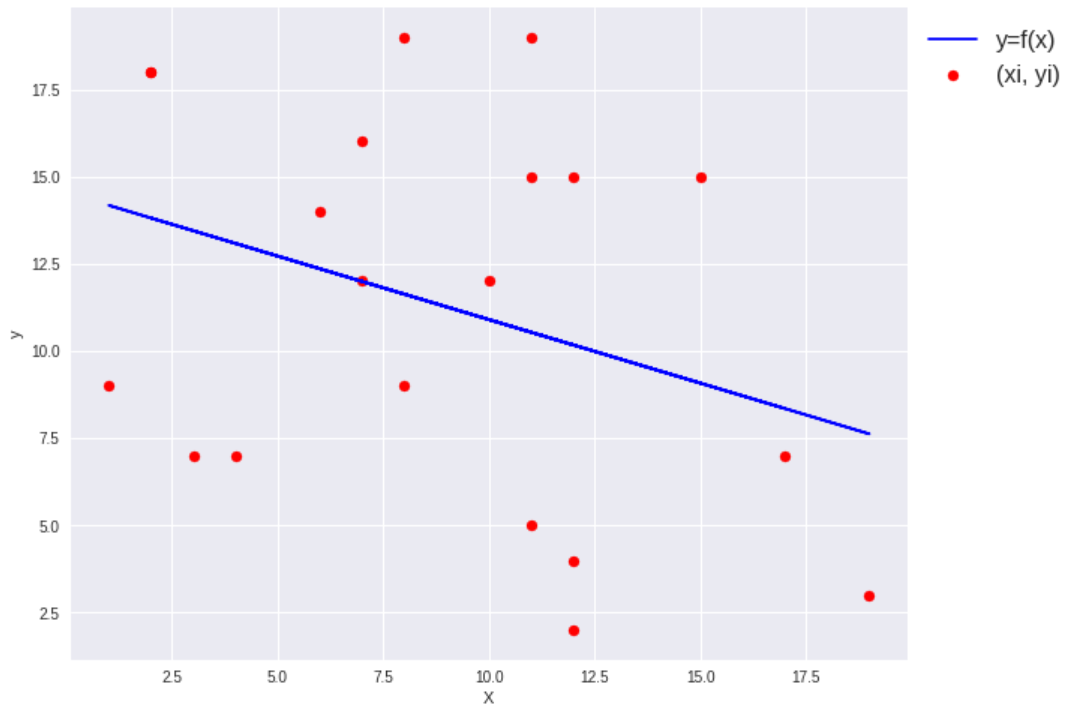
ランダムに生成したデータの為、 $(x_i,y_i)$ に直線的な関係は感じられないものになっていますが、それに対して直線を当てはめられています。

ちなみにScikit-learnを使って実装すると以下のようになります。

from sklearn.linear_model import LinearRegression

# modelに入力可能な二次元配列にする
X = np.array([[x] for x in X])

model = LinearRegression()
model.fit(X, y)

preds = model.predict(X)

同様にグラフにプロットします。

fig = plt.figure(figsize=(10,8))
plt.style.use('seaborn')
plt.scatter(X, y, c='r', label='(xi,yi)')
plt.plot(X, preds, 'b', label='y=f(x)')
plt.xlabel('X')
plt.ylabel('y')
plt.legend(loc='upper left', bbox_to_anchor=(1,1), fontsize=16)
plt.show()

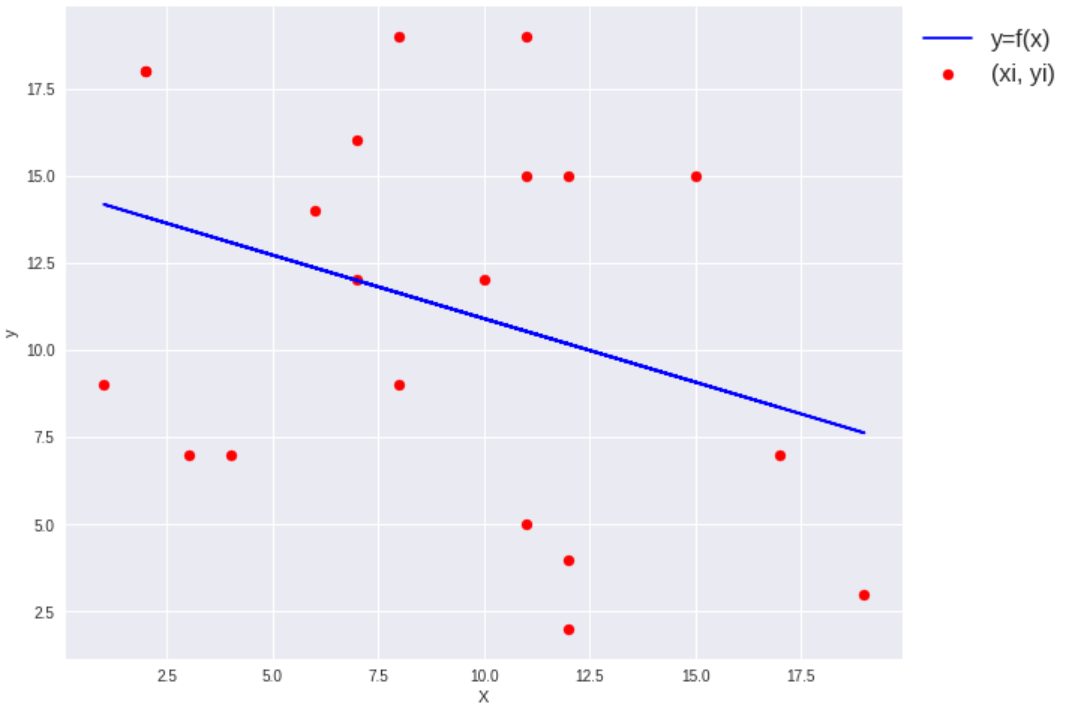
先程と同様に直線を当てはめられました。

尤もらしい直線である、関数 $y=f(x)$ と $(x_i,y_i)$ との $y$ 方向の誤差の二乗和（二乗誤差） $\sum_{i=1}^ n(y_i - Ax_i - B)^ 2$ を最小化するのが、最小二乗法です。すなわち関数をデータに当てはめた結果の二乗誤差が最小になるパラメータ（傾き $A$ と切片 $B$ ）を推定する方法になります。

ここでいう誤差はグラフのこの部分になります。

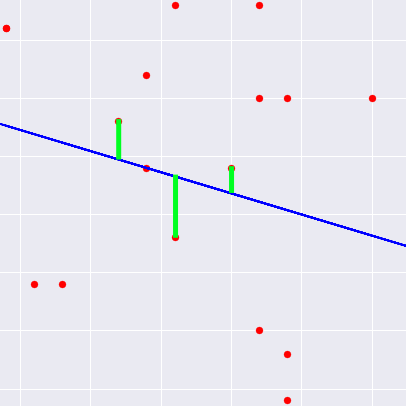
全ての点に引くと見づらくなるため3つの点だけに引いてますが、この $y$ 方向の誤差を最小化する、尤もらしい直線を求めるのが最小二乗法になります。

尤もらしい直線である、関数 $y=f(x)$ が意味するものの直感的な理解としては、説明変数（ $x$ ）を元に目的変数（ $y$ ）を説明するに当たって、 $x$ と $y$ になるべく近い形で直線を通し、先程解説した誤差を最小化していく、というようなイメージです。

データセットを使ってフィッティング

次に実データを使って、分析してみます。

KaggleのHeights and weightsデータセットを使います。

ではデータを読み込んで、表示します。

import pandas as pd

dataset = pd.read_csv(
    'heights_and_weights/data.csv',
    dtype={
        'Height': np.float32,
        'Weight': np.float32
    }
)
display(dataset.head())

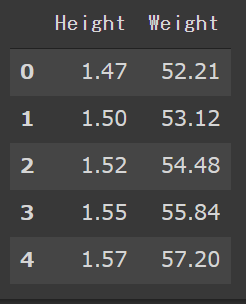
このデータセットはこのように身長と体重がペアになったデータセットです。

今回は身長を説明変数、体重を目的変数として、体重を説明する直線を引いていきます。

# 先程書いた関数群をクラス化した回帰モデル

class LeastSquaresMethod(object):
    
    @staticmethod
    def covariance(X, y):
        X_deviation = X - X.mean()
        y_deviation = y - y.mean()
        cov = (X_deviation * y_deviation).mean()
        return cov

    @staticmethod
    def variance(X):
        var = ((X - X.mean()) ** 2).mean()
        return var

    @classmethod
    def least_squares_method(self, X, y):
        A = self.covariance(X, y) / self.variance(X)
        B = y.mean() - A * X.mean()
        return A, B

    @classmethod
    def f(self, X, y):
        A, B = self.least_squares_method(X, y)
        return A*X + B

上のLeastSquaresMethodクラスを使って、データにフィッティングし、結果をプロットします。

X = dataset['Height'].to_numpy()
y = dataset['Weight'].to_numpy()

preds = LeastSquaresMethod.f(X, y)


fig = plt.figure(figsize=(10,8))
plt.style.use('seaborn')
plt.scatter(X, y, c='r', label='(Heights,Weights)')
plt.plot(X, f(X, y),, 'b', label='y=f(x)')
plt.xlabel('X')
plt.ylabel('y')
plt.legend(loc='upper left', bbox_to_anchor=(1,1), fontsize=16)
plt.show()

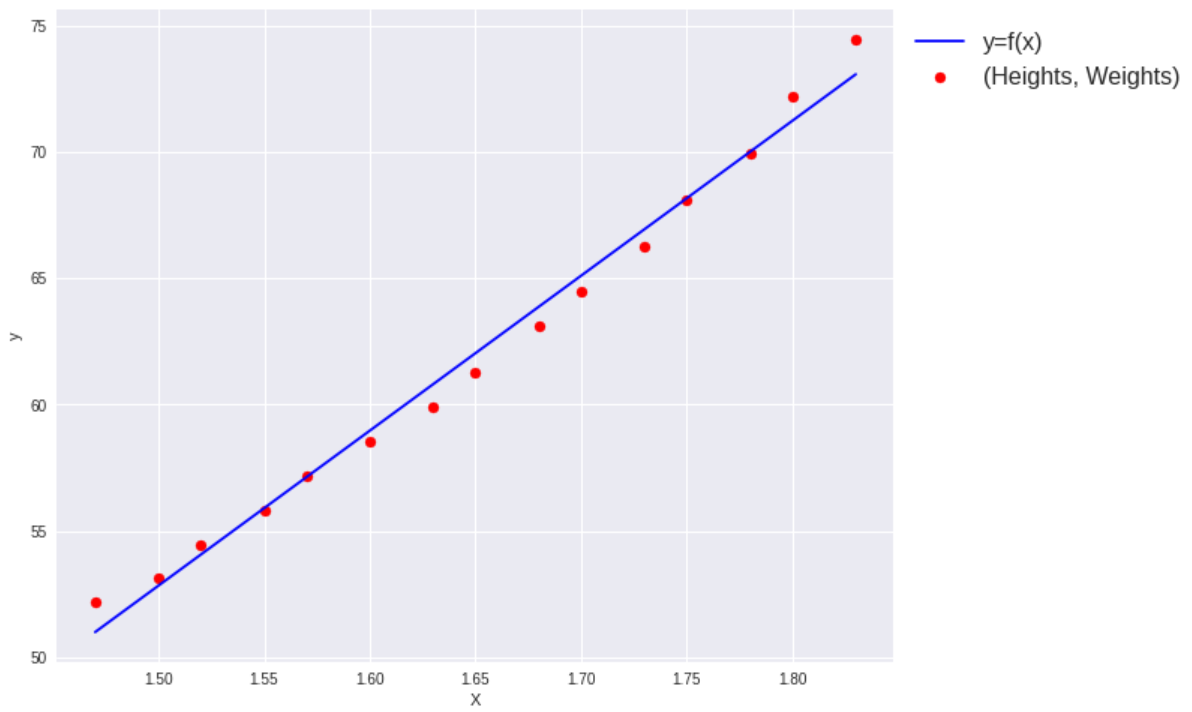
尤もらしい直線が引けています。次に回帰モデルの出力をデータに加えて眺めてみます。

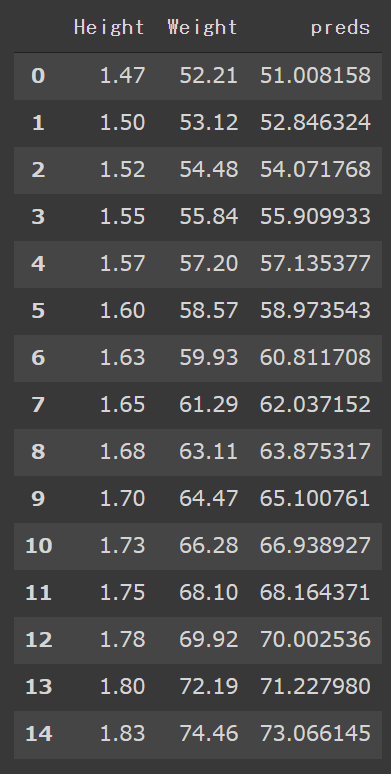
目的変数である体重データと比較して、体重データの説明として良い結果が出力出来ているように見えます。

次にこの回帰モデルの性能を評価するため、回帰の評価指標である決定係数( $R^ 2$ )を使って、実際に評価します。

決定係数( $R^ 2$ )

$\displaystyle{ {R^{2}} = 1 - \frac{ \sum_{i=1}^{N} { ( {y}_i - \hat{y}_{i} ) }^{2} }{ \sum_{i=1}^{N} { ( {y}_i - \bar{y}) }^{2} } }$

$y_i$ : 各レコードのデータ

$\hat{y_i}$ : 各レコードに対するモデルの予測値

$\bar{y}$ : $y$ の平均値

決定係数は最大が1で、1に近いほど良い当てはまりが出来ていて、性能が高いと考えられます。

ちなみに、この決定係数を最大化することはRoot Mean Squared Errorを最小化することと等価でもあります。

決定係数をPythonでスクラッチ実装した場合、以下のようになります。

def r2_score(y_true, y_pred):
    return  1 - ((y_true - y_pred) ** 2).sum() / ((y_true - y_true.mean()) ** 2).sum()

目的変数である体重データと、回帰モデルの出力結果を評価指標に通してみます。

r2_score(y, preds)

[output] 0.9891969224457968

決定係数のスコアからもかなり当てはまりのよい結果になりました。

最小二乗法は $y$ 方向の誤差を最小化する特性から、極端な外れ値がデータに含まれている場合、そこに引っ張られる形で、外れ値の影響を大きく受ける特性となっています。（大幅な外れ値を含むこと、すなわち平均値に大幅な変動が起きます。）このデータセットはグラフからも見れる通り、データにはっきりとした直線的関係をある為、きれいに直線を当てはめられていて、且つスコアもよいものとなっております。

データセットを分割して検証

次に先程使ったデータセットを訓練データとテストデータに分割し、訓練データにフィッティングさせたあとに、回帰モデルにとって未知データであるテストデータで性能評価をします。回帰モデルであるLeastSquaresMethodクラスもそれに合わせて作り変えます。

# 訓練用を8件、テスト用を7件に分割する
X_train = X[:8]
X_test = X[8:]
y_train = y[:8]
y_test = y[8:]

訓練データから得たパラメータ（ $A,B$ ）を保持し、テストデータの説明変数（ $x$ ）のみを与えて、関数 $y=f(x)$ を予測させる形に実装します。

# 保持しておくパラメータの定義と、
# fitメソッドとpredictメソッドを追加

class LeastSquaresMethod(object):
    def __init__(self):
        self.A = 0
        self.B = 0
    
    @staticmethod
    def covariance(X, y):
        X_deviation = X - X.mean()
        y_deviation = y - y.mean()
        cov = (X_deviation * y_deviation).mean()
        return cov

    @staticmethod
    def variance(X):
        var = ((X - X.mean()) ** 2).mean()
        return var

    def least_squares_method(self, X, y):
        A = self.covariance(X, y) / self.variance(X)
        B = y.mean() - A * X.mean()
        return A, B

    def fit(self, X, y):
        self.A, self.B = self.least_squares_method(X, y)

    def predict(self, X):
        return self.A*X + self.B

model = LeastSquaresMethod()
model.fit(X_train, y_train)

まず、先程フィッティングした、訓練データに対する出力結果をプロットしてみます。

preds = model.predict(X_train)

データセット全件の時と同様に、尤もらしい直線が引けています。

次にテストデータを予測させて、出力結果をプロットしてみます。

preds = model.predict(X_test)

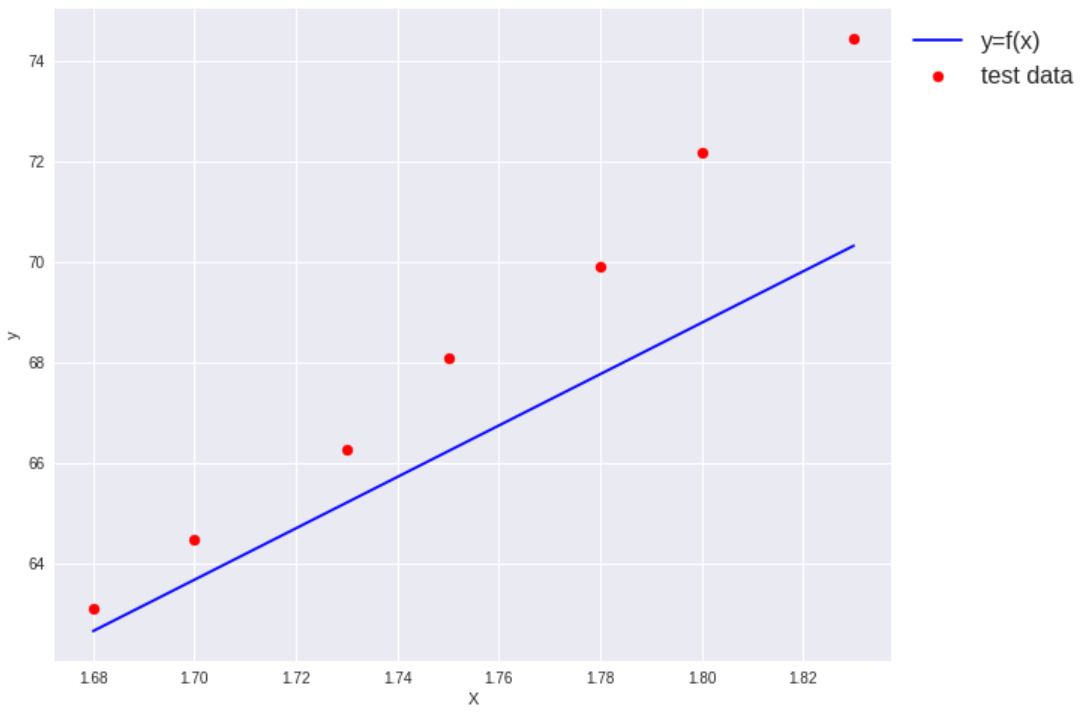
テストデータを予測させた結果、先程のような尤もらしい直線ではなくなりました。

次にこの結果を決定係数に通してみます。

r2_score(y_test, preds)
[output] 0.617812842130661

決定係数のスコアもだいぶ下がりました。

訓練データにフィッティングし、取得したパラメータを元にテストデータを予測させた結果になります。

これがこの回帰モデルの未知データに対する汎化性能と言えます。

ひとまず、説明変数のみから、関数 $y=f(x)$ を予測することができました。

以上で最小二乗法の解説は終わりになります。